Mérnökként elsődleges feladatunk a tartós javak mellett szépet is alkotni. De mi is a szépség? Hiszen ez a fogalom igencsak szubjektív. A tudományos módszerekkel való méréséhez azonban elég az aranyarány törvényét ismerni.
Az első geometriai meghatározást Eukleidész alkalmazta az isteni arányra. Két rész (a és b, a>b) akkor aránylik egymáshoz az aranymetszés szerint, ha az egész (a+b) úgy aránylik a nagyobbik részhez (a), ahogy a nagyobbik rész (a) a kisebbhez (b). Mivel matematikailag „bonyolult” levezetni, így hétköznapibb értelemben a 2/3 – 1/3 részre osztással kapjuk meg a kérdéses aránypárt. A divina promortione néven is ismert metszés a természetben és a művészetekben is gyakran jelenik meg, akárcsak egy másik, hozzá meglehetősen közeli számsor tagjai is.
A 13. században Fibonacci megalkotta a mérvadó számtani sort, melyben minden számot az előző kettő összegeként kapunk meg. 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13. Érdekessége, hogy a számok növekedésével a két egymás melletti elem aránya egyre jobban közelít az aranymetszés arányához, melyet a Φ fejez ki. Értéke pedig a 1,618.
Pl. 21/13=1,615385
377/610=1,618037
Na de mi köze mindennek a természethez?
A nagyobb léptékekből indulva megláthatjuk, hogy a világunkat alkotó galaxisok jó részének képei követik a Fibonacci számsor alapján szerkesztett spirált. A szabályos galaxisok egyik nagy csoportjának már a neve is utal a különleges jelenségre, ezek a spirálgalaxisok. Maga a Tejútrendszer is ezen csoportba tartozik, a megközelítőleg gömb alakú magját körülvevő porfelhőben helyezkednek el a spirálkarok, amik fiatal csillagokból és csillagközi anyagokból állnak. Beljebb haladva akár a Szaturnusz bolygó gyűrűje is felosztható az aranymetszést idéző részekre. De górcsövünk alá véve a Földet, azon belül is az embert, temérdek számú ilyen aránnyal találkozhatunk. Csak felületesen érintve a témát elég megfigyelni az arcunkat. A szemek és a száj harmadolják az ábrázatunkat, és minél tökéletesebb ez a felosztás, annál „szebbnek” fogjuk tekinteni a fürkészett alanyokat. A fül? Önmagáért beszél. Akár csak a galaxisok spiráljai, ezekre is szépen ráilleszthető a Fibonacci spirál.
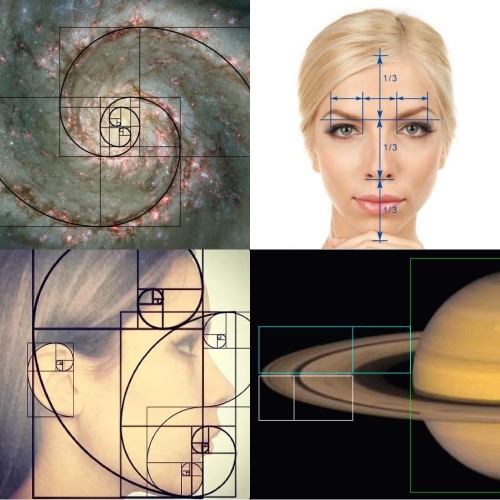
Forrás:
https://blogs.unimelb.edu.au/sciencecommunication/2018/09/23/the-universe-in-a-spiral/
https://hu.pinterest.com/pin/58476495137470546/
https://hu.pinterest.com/pin/440860251023006486/
https://www.goldennumber.net/solar-system/
A növényvilágot kémlelve megtalálhatjuk az őket uraló Fibonacci számokat. A virágszirmok, a porzók, de még a levelek is leggyakrabban hármasával, ötösével rendeződnek. A rózsák esetében a csészelevelek száma is pontosan öt. A tobozok korongján a középponttól jobbra és balra az aranymetszés spirálja rajzolódik ki. Ugyanígy a napraforgók fején a termések.
Az állatvilág se mentes a matematikai tökéletességektől. Az ötkarú tengericsillag pentagramot formáz, melynek átlói úgy metszik egymást, hogy mindegyik a másik átlót az aranymetszés szerint osztja fel. A csigák meszes házainak felépítése csigavonalat követ – az elnevezés is innét ered –, mely alapjául szintén a korábban már taglalt Fibonacci- vagy másik nevén aranyspirál szolgál. Ugyanez figyelhető meg a macskák karmain, a papagájok csőrén és még sok máson állaton is. Kicsit visszakacsintva a növényekhez, többnek a levele térbeli csigavonal mentén rendeződik el.

Az ember csupán mindezen csodák kópiáját teremtheti meg, mi csak tanulhatunk abból, amit a természet már megalkotott, és megpróbálhatjuk felvenni vele a versenyt.
Forrás:
https://hu.pinterest.com/pin/444589794471639170/
https://hu.pinterest.com/pin/161707442855751898/
https://hu.pinterest.com/pin/544302304947822285/
https://hu.pinterest.com/pin/457467274619564132/
https://clevelanddesign.com/insights/the-nature-of-design-the-fibonacci-sequence-and-the-golden-ratio/
https://www.cymascope.com/cyma_research/biology.html


