Számok, amik annyira hatalmasak, hogy leírásához még az univerzum is kevés lenne (még akkor is, hogyha a számjegyeik csupán molekula méretűek lennének).
Sokszor szólnak arról cikkek, hogy sikerült felfedezni az eddig ismert legnagyobb prímszámot (jelenleg a 2024 októberében felfedezett 41 024 320 számjeggyel büszkélkedő 2¹³⁶ ²⁷⁹ ⁸⁴¹ − 1 M136279841 jelű szám számít a legnagyobb ismert prímnek). Viszont már általános iskolában megállapítást nyer az a tény, hogy a számsík mind pozitív, mind negatív irányban végtelen, ennek ellenére az M136279841-hez hasonlóan vannak olyan irgalmatlanul nagy számok, amelyeknek a könnyebb (vagy gyorsabb) leírás érdekében inkább nevet kaptak. Ennek is köszönhető, hogy a tudományos világ sok ismert, névvel rendelkező racionális, vagy irracionális számot tart nyilván, mint a π, vagy az Euler-szám. De ezeken felül is a cikk címének megfelelően vannak nagyon nagy megnevezett számok, amelyek annyira nagyok, hogy semmilyen létező példa nem található rájuk.
Googol, googolplex
Ilyen nagy ismert számnak fogható fel például 1 googol, amely 10 századik hatványának felel meg és nem mellesleg jóval nagyobb szám, mint az univerzumunkban fellelhető összes atom (ami amúgy körülbelül 10^80 és 10^87 közé tehető). A köztudatban 1 googolon kívül még ismert a 10 googolodik hatványa, a googolplex ami 10^googol, vagy hatványozva leírva -nak számít.
Tény, hogy már 1 googol-nak (már csak a nagyságából kiindulva) a gyakorlati fizikában semmilyen jelentősége nincs, viszont vannak olyan elméleti a kombinatorikai és a valószínűségszámítások, amelyek megoldásához képest nemhogy 1 googol, de még egy googolplex is eltörpül.
A Shannon-szám
Ilyen számként fogható fel a sakk összes kimenetelét összegző Shannon-szám, amely úgy körülbelül 10^120-nak felel meg. Viszont a logikus számítások alapján ebből a számból csupán csak töredék ( , vagy szebben kifejezve 3,7*10^43) számít indokolt lépésnek.
A Skewes-szám
Tény, hogy a Shannon-szám „csak” egy googolnál nagyobb, de a Skewes-szám akár 1 googolplex-et is le tudja körözni, attól függ, hogy hogyan értelmezik a Riemann sejtést, amely a prímszámok egyenletes elosztását állítja.
Mármost a Skewes szám egy határértéknek számít, arra a legkisebb számra, ami után a prímszámláló függvény és a logaritmikus integrál függvény viszonya először megfordul. Ez az érték 10^316 körül van/lehet.
A Graham-szám
A következő szám egy szinte érthetetlen kérdés leírhatatlan válasza.
Köszönhető ez annak, hogy a kérdés valahogy így szól: ha egy n dimenziójú hiperkocka éleit pirosra vagy kékre színezzük, akkor vajon mindig megjelenik-e egy bizonyos konfiguráció (például egy teljesen összekötött részgráf, amelynek minden éle azonos színű)?
Ennek az n számnak a felső korlátja a G-vel jelölt Graham-szám, amely annyira szürreálisan hatalmas szám, hogy még „közönséges hatványozással” sem lehet kifejezni. A szám leírásának első lépéséhez a Knuth-féle nyíljelölést kell bevezetni, amely az alábbi módon működik:
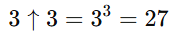
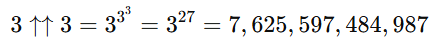
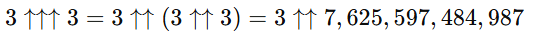
Mármost látható, hogy már a háromnyilas hatványozás is 1 googol értékét fogja meghaladni a 3 7.625.597.484.987-szeres összeszorzásánál. Ehhez képest a Graham-számhoz vezető első lépéshez négynyilas hatványozást kell alkalmazni, amely annyit jelent, hogy háromszor egymás után kell a háromnyilas hatványozást elvégezni. Ezáltal kapható meg a értéke.
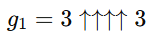
Ami már önmagában sokkal nagyobb, mint 1 googolplex. Azért g1 a jelölés, mivel a g2-nél pedig a háromnyilas hatványozás történik g1-szer.
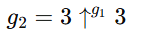
A g3-nál pedig szintén ugyanez a helyzet, csak ott a kapott értéket g2-ször hatványozzák.
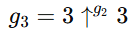
A Graham -szám ehhez képest g64 értékének felel meg. Ebből is látszik, hogy egy irdatlanul nagy számról van szó.
Annyira nagy, hogy valódi értékét soha senki nem fogja tudni kiszámolni, vagy leírni. Annyira nagy, hogy már a számjegyei pontos számát sem lehet az átlagos matematikai jelekkel kifejezni. Számításokkal az utolsó 500 számjegyét meg tudták fejteni. A Graham-szám számít minden idők legnagyobb matematikai megoldásának.
Számok, amik még a Graham-számnál is nagyobbak
Természetesen az idők során keletkeztek a Graham-számnál sokkal nagyobb számok (TREE(3), Busy Beaver(n) ), de ezeknek a számoknak, vagy inkább függvényértékeknek a gyakorlatban már nincsen különösebb jelentőségük.
Különösen igaz ez a legnagyobb elnevezett számra, a Rayo-számra. A számot egy 2007-es matematika versenyen definiálta Agustín Rayo mexikói matematikus. A definíciója szerint a szám az a legkisebb szám, amelyet nem lehet leírni egy n hosszúságú kifejezéssel a szokásos matematikai jelkészlet segítségével.
Tehát a szám annyira hatalmas, hogy lehetetlen kifejezni. Ennél a számnál merülhet fel a kérdés, hogy ez vajon még tudomány, ezotéria, önreklámozás, szemfényvesztés, vagy matematikai perverzió.


